Autor: Dr. Joaquín M. Prada Jiménez de Cisneros
En mi artículo de enero de este año, al que se puede acceder aquí hablaba sobre uno de los modelos matemáticos más sencillos y usados en epidemiología: el modelo SIR (Susceptible-Infectado-Recuperado). Este modelo es simple de implementar resolviendo las ecuaciones diferenciales que lo componen. Como mencioné en el artículo anterior, se pueden resolver tanto analíticamente como numéricamente. Recomiendo su breve lectura, dado que este artículo extiende los conceptos ya mencionados.
Vamos a asumir una enfermedad con un número básico de reproducción (R0) igual a 2, esto quiere decir que cada infección producirá dos casos secundarios cuando la población es completamente susceptible. En el ejemplo que vamos a ver aquí, la infección perdura dos semanas (14 días), por lo que la tasa de recuperación diaria es 1/14. Simulando 300 días (alrededor de 10 meses), podemos observar el pico de la epidemia un poco después del día 100 (Figura 1 – línea roja). En este ejemplo, el pico de la epidemia tiene a casi el 16% de la población infectada simultaneamente. El porcentaje de la población susceptible al final de la simulación (día 300) ronda el 20%, con el 80% de la población recuperada (Figura 1 – líneas verde y amarilla respectivamente). Esto significa que el 80% de la población ha sido infectada a lo largo de la epidemia.
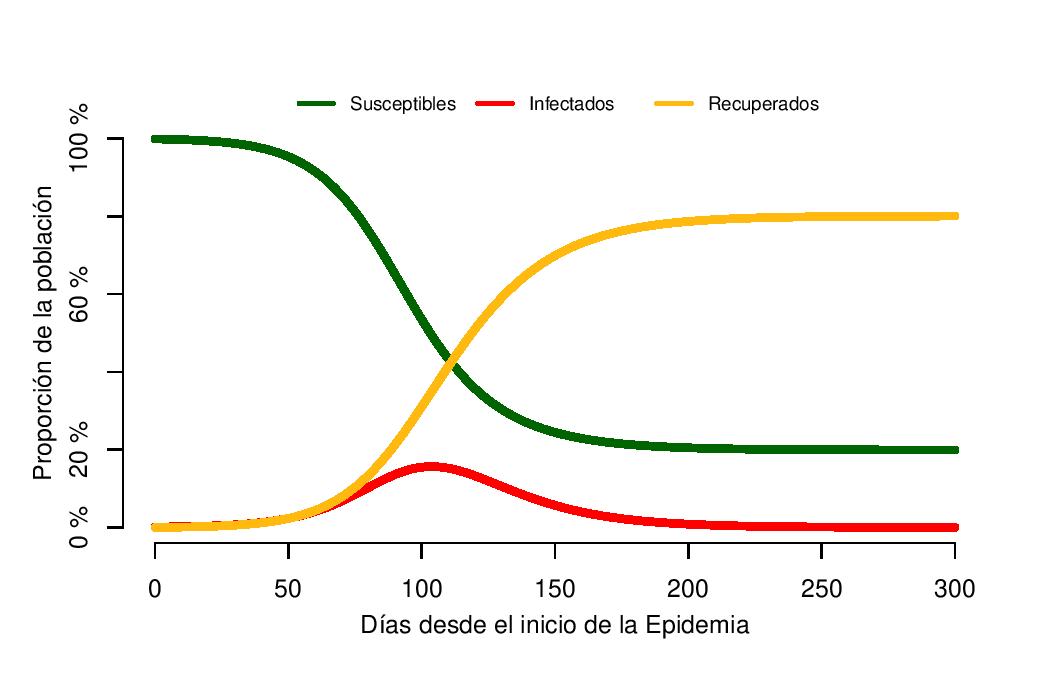
Figura 1: Dinámica de un modelo SIR, con R0=2 y tasa de recuperación = 1/14. La mayoría de la población empieza susceptible, y a lo largo de los 300 días se irían infectando y recuperando. El pico de la epidemia es alrededor del día 105, con el 16% de la población infectada.
Vamos a explorar ahora un escenario donde vacunamos a parte de la población en respuesta a la epidemia. Asumimos que tenemos una vacuna con una eficacia del 90%: vamos a usar un “todo o nada”, el 90% de los vacunados estarán protegidos y para el 10% restante la vacuna no tendrá ningún efecto. El efecto de la vacuna es instantáneo e independiente del estado del individuo (susceptible, infectado, etc.). Asumimos igualmente que la campaña de vacunación transcurre en el día 100 desde el inicio de la epidemia, todos los individuos son vacunados el mismo día, independientemente de si han tenido la infección ya o no, y la cobertura es del 50%. El resultado de este escenario se puede ver en la figura 2. El 45% de la población está vacunada (y protegida), la población que sigue susceptible sería, como en el escenario anterior, alrededor del 20%, pero ahora a lo largo de la epidemia alrededor del 54% de la población ha tenido la infección (en lugar del 80% de antes). Este número se obtiene del 35% que están recuperados al final de la epidemia (Figura 2 – línea amarilla) más los recuperados e infectados antes del día 100 que fueron exitosamente vacunados y son inmunes.
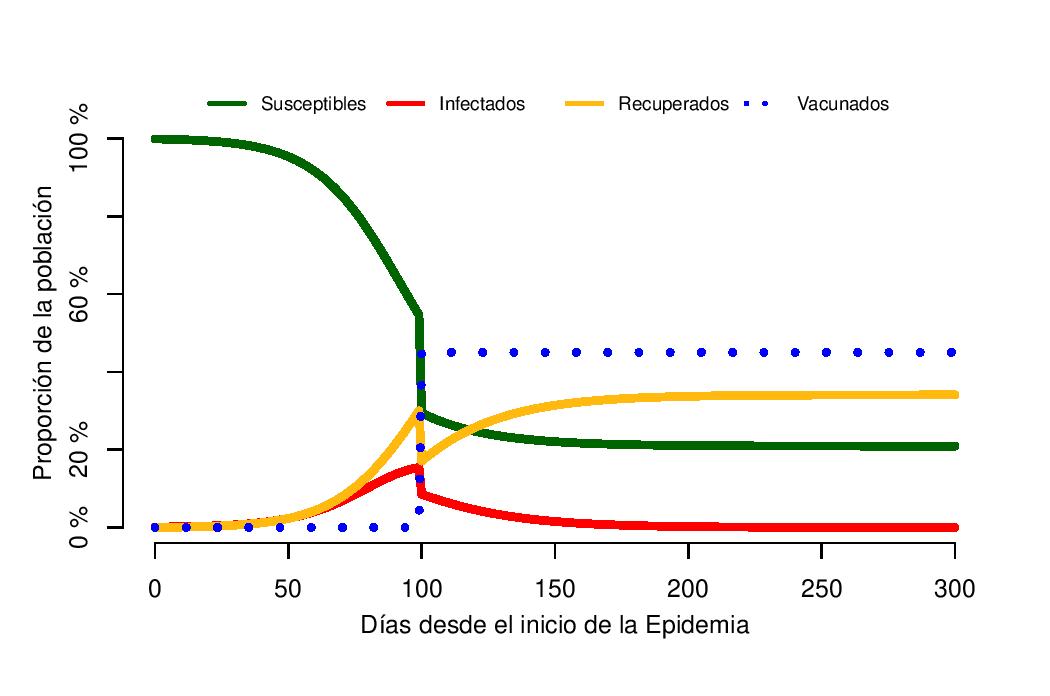
Figura 2: Dinámica de un modelo SIR, con R0=2 y tasa de recuperación = 1/14. Una vacunación efectiva del 45% (covertura 50%, eficacia 90%) ocurre el día 100 en la población. El pico de la epidemia ocurre el día 100, con el 15.4% de la población infectada.
¿Qué hubiera pasado si la vacuna hubiera sido distribuida antes, por ejemplo el día 50 en lugar del día 100? En ese caso, el pico de la epidemia tendría un máximo del 2.1% de la población infectada, este pico ocurriría en el día 50, justo antes de la vacunación (Figura 3 – línea roja). Después de la vacunación el número de casos sería bajo durante el resto de la epidemia, con un número total de individuos infectados durante los 300 días por debajo del 20% de la población. El porcentaje de la población susceptible rondaría el 40% (Figura 3 – línea verde).
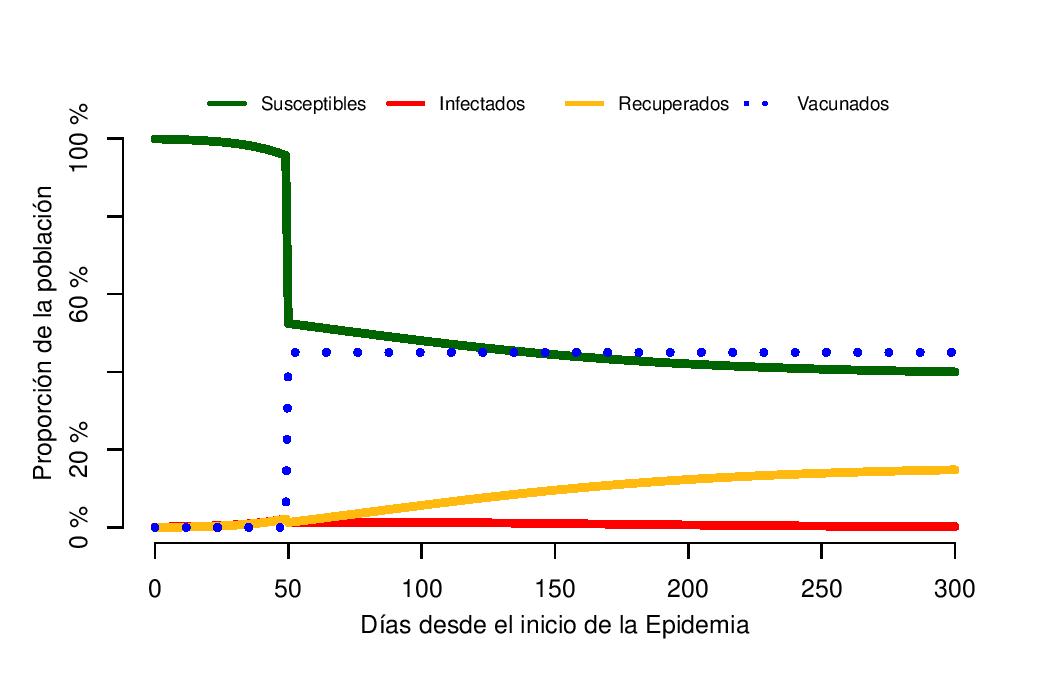
Figura 3: Dinámica de un modelo SIR, con R0=2 y tasa de recuperación = 1/14. Una vacunación efectiva del 45% (covertura 50%, eficacia 90%) ocurre el día 50 en la población. El pico de la epidemia ocurre el día 50, con el 2.1% de la población infectada.
Escenarios como los presentados aquí son interesantas para evaluar la trayectoria de una epidemia. Obviamente, los ejemplos anteriores son relativamente simples: se asume que tanto la campaña de vacunación, como el efecto de la vacuna, son instantáneos. Estamos asumiendo también que los individuos infectados serán luego inmunes, lo cual es razonable cuando la duración de la inmunidad es mayor que el periodo simulado (en este caso 300 días). Los modelos mostrados aquí son determinísticos, es decir, la solución es siempre la misma mientras los parámetros usados no cambien. Esto significa que no hay estocasticidad (por ejemplo, eventos fortuitos), aunque este efecto sea muy importante a niveles bajos de prevalencia de casos. De todas maneras, estos escenarios destacan aspectos clave de la dinámica de la epidemia, como que no es solo importante la covertura de una campaña de vacunación, sino también cuando ocurra.
Otro aspecto destacable es que una campaña de vacunación temprana, además de minimizar el pico de la epidemia, alarga la duración de esta. Aunque no es muy visible en las figuras anteriores, sin campaña de vacunación, 300 días después del inicio de la epidemia, el porcentaje de la población actualmente infectada es solo del 0.01%, lo cual indicaría que la epidemia ha casi concluido. Sin embargo, en el ejemplo con la vacunación en el día 50, el porcentaje de la población aún infectada en el día 300 es casi del 0.2%, lo cual es 20 veces mayor. Hay que recordar que a pesar de que este porcentaje de casos es mayor en el día 300, a lo largo de la epidemia hemos tenido muchos menos infectados. Es más, en ambos casos la epidemia estaría en vias de extinción, pero el número de casos después de los primeros 300 días sería distinto.
Actualmente, modelos basados en estos conceptos se usan para informar salud pública, incluida la respuesta a la epidemia de COVID19. Como mencioné en el artículo anterior, muchos de los modelos usados inicialmente estaban basados en modelos de gripe (generalmente SEIRS: Susceptible-Expuesto-Infectado-Recuperado-Susceptible), donde la duración de la immunidad es temporal y específica a las distintas variantes. Uno de los mayores desafíos para los modeladores es desarrollar modelos que reproduzcan apropiadamente las dinámicas observadas y los procesos biológicos clave, sin complicarlos de manera excesiva. Para esto seguimos el principio de parsimonia de la navaja de Ockham: “en igualdad de condiciones, la explicación más sencilla suele ser la más probable”.