– Autor: Dr. Joaquín M. Prada Jiménez de Cisneros.
A finales del 2019, cuando la epidemia del COVID estaba todavía limitada a un cúmulo de casos en China y no era aún la pandemia global que ocupa la mayor parte de las noticias de hoy, tuve el placer de dar una charla sobre epidemiología en Crevillente. Agradecido por la invitación del Dr. Daniel Belmonte y la Dra. Ana Satorre, el 23 de diciembre, en la Casa de Cultura del Ayuntamiento de Crevillent, conversamos sobre enfermedades infecciosas y cómo las matemáticas pueden ayudar a informar intervenciones en salud pública.

A día de hoy, muchos de nuestros ávidos lectores estarán familiarizados, al menos en parte, con los “modelos matemáticos” que se están usando para la respuesta contra el COVID. Pero ¿cómo funcionan exactamente? Como toda buena historia, hay que empezar por el principio, que es la definición de “Epidemiología”: según el centro para el control y la prevención de enfermedades (CDC en inglés), es el estudio y análisis de la distribución (quién, cuándo, dónde) y determinantes de condiciones de salud y enfermedad en un grupo poblacional definido.
En el caso de enfermedades infecciosas, sabemos que una infección pasará de individuos infectados a individuos susceptibles. Quizás el modelo más sencillo y más utilizado para explicar modelos matemáticos es el mostrado en la Figura 1a. Imaginemos una enfermedad que confiere inmunidad despúes de una infección, el clásico ejemplo es el sarampión. Podemos separar los individuos de la población en tres grupos: los individu@s que nunca han tenido la infección y son susceptibles (S), los individu@s que están actualmente infectados (I), y por último los que ya la han tenido y se han recuperado, siendo en consecuencia inmunes (R). Durante una epidemia, los individuos pasarán del grupo de susceptibles al de infectados y eventualmente al de los inmunes. La rapidez con la que esto ocurre se llama «tasa de transmisión» (de S a I) y «tasa de recuperación» (de I a R), respectivamente. En realidad, esta ilustración está escondiendo tres ecuaciones diferenciales ordinarias, que se pueden resolver tanto analítica como numéricamente.
Obviamente, podemos cambiar las configuraciones de los grupos en los que dividimos la población y como están relacionados entre sí en función de la enfermedad de interés. Otras configuraciones muy comunes son SIS (susceptible-infectado-susceptible) o SEIS (susceptible-expuesto-infectado-susceptible) como se puede ver en la Figura 1b y 1c. Los primeros modelos de COVID por ejemplo estaban basados en modelos de gripe. Es importante tener en cuenta que estos modelos son simples abstracciones con ciertas limitaciones. En particular, se asume que la población es homogénea (es decir, no hay diferencias entre individuos y los contactos entre todos son iguales), y que todos los individuos son susceptibles. A pesar de estas simplificaciones, estos modelos reproducen relativamente bien las dinámicas que se observan en la realidad.
Otro concepto del que se ha hablado en la prensa recientemente es el número básico de reproducción (R0); en nuestro modelo SIR se calcula simplemente dividiendo la tasa de transmisión entre la tasa de recuperación. Este valor es el número esperado de casos secundarios producidos por una infección única en una población completamente susceptible. Por lo tanto si es superior a uno, vamos a tener una epidemia, mientras que si es menor a uno, la infeción desaparecerá de la población sin causar una epidemia. ¿Qué ocurre si vacunamos a una parte de la población (de forma que tienen inmunidad)? Entonces ya no estamos en una situación donde toda la población es susceptible. Ahora hablaríamos del número de reproducción efectivo (RE), siendo este un número que oscila con los cambios poblacionales, campañas de vacunación, etc. (Figura 2).
El número de reproducción efectivo está relacionado con otro concepto, del que también se ha hablado en la prensa, que es el de la inmunidad colectiva. Esto es una forma de protección indirecta de enfermedades infecciosas cuando una gran parte de la población es inmune a la infección. Conceptualmente, podemos calcular el nivel de vacunación crítico, que es la covertura necesaria para que nuestro número de reproducción sea menor a uno, para así evitar epidemias. Este nivel crítico se calcula simplemente con la siguiente ecuación: 1 – 1/R0. Volviendo al ejemplo del sarampión, el R0 está alrededor de 15, por lo que necesitariamos inmunizar como mínimo (con una vacuna perfecta) al 93% de la población. Es importante recordar que estamos hablando de escenarios donde la vacuna confiere inmunidad permanente, lo cual es algo generalmente aceptado para enfermedades como el sarampión. La vacunación, por lo tanto, no solo protege al individuo, sino que ademas ayuda a proteger al resto de la población. Si pensamos en individuos inmunocomprometidos o que no responden a la vacuna, la única esperanza de no sufrir de estas enfermedades completamente evitables, es que el resto de los individuos en la población se vacunen.
La importancia de la vacunación no es nada nuevo. De hecho, la primera campaña de vacunación global, cubriendo varios continentes, fue la Real Expedición Filantrópica de la Vacuna (1803-1806). La misión fue dirigida por el doctor alicantino Francisco Javier de Balmis, que recorrió la mayor parte del continente americano y las Filipinas vacunando contra la viruela, enfermedad que causaba estragos en las poblaciones locales. Esta expedición era muy complicada logísticamente, y dado que no se podía mantener la cadena de frío necesaria para la vacuna, se utilizó a niños que fueron siendo inoculados por turnos durante el viaje. El segundo cirujano a bordo, el doctor José Salvany y Lleopart, no sobrevivió al viaje y fallecio en Cochabamba en 1810. A pesar de que a día de hoy esta expedición haya caído casi en el olvido -salvo los homenajes puntuales que se le hicieron en 2019 por su centenario-, los contemporaneos del Dr. Balmis, como el Dr. Edward Jenner, que desarolló esa vacuna de la viruela unos años antes, solo tenían palabras de admiración (cit.): “No puedo imaginar que en los anales de la Historia se proporcione un ejemplo de filantropía más noble y más amplio que este”.
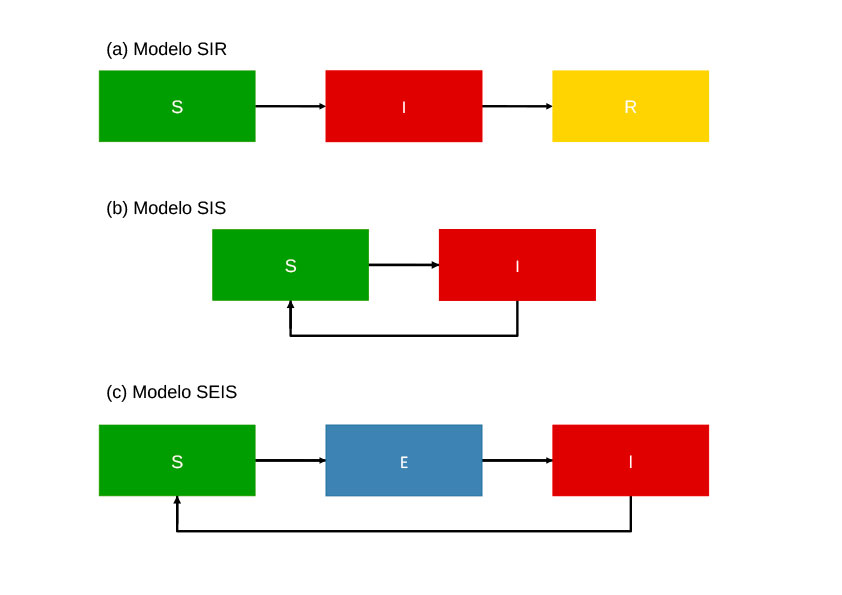
Figura 1: Diagramas de modelos determinísticos a nivel poblacional. (a) modelo SIR – susceptibles-infectados-recuperados. La población está dividida en tres grupos, acabando todos los individuos que han sido infectados en el grupo de los recuperados, los cuales son inmunes. Este modelo representa enfermedades como el sarampión o la viruela. (b) modelo SIS – susceptibles-infectados-susceptibles. Los individuos son susceptibles otra vez después de una infección. (c) modelo SEIS – susceptibles-expuestos-infectados-susceptibles. Aquí consideramos un grupo de expuestos, que aunque ya han sido infectados, no son infecciosos aún (es decir, no son considerados para la transmisión).
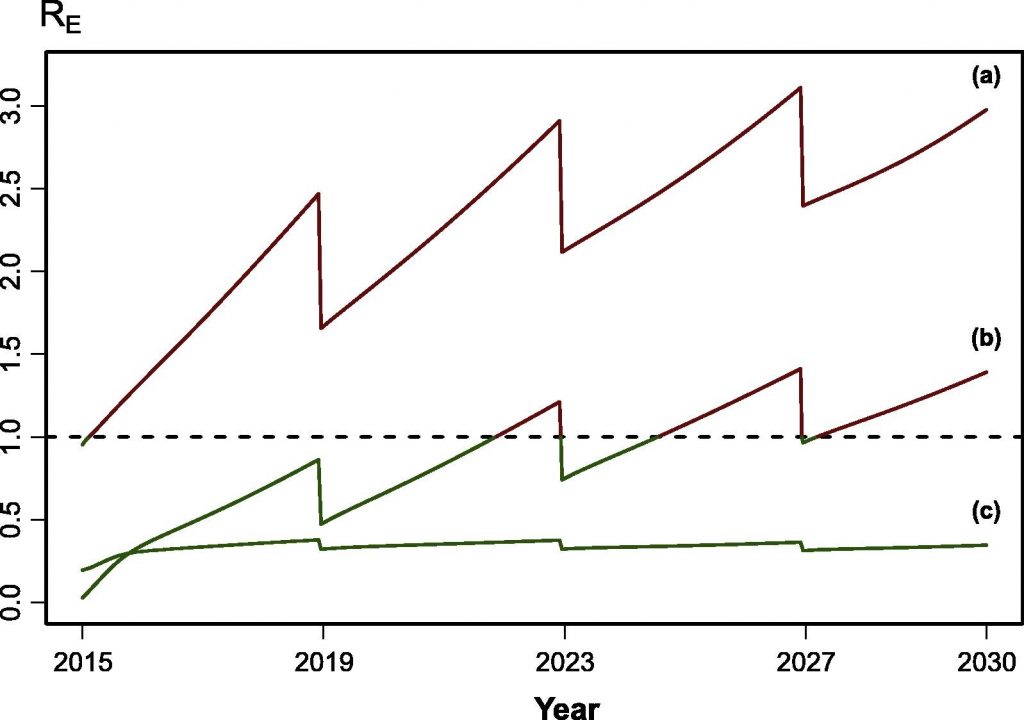
Figura 2: Ejemplos de cambios en el número de reproducción efectivo. (a) RE oscila con un valor superior a 1, por lo que siempre habría epidemias en esta población. (b) RE oscila alrededor de 1, por lo que dependiendo de cuando se introduzca la infección, podría haber una epidemia. (c) RE es consistentemente menor a 1, por lo que nunca habría epidemias en esta población. Imagen extraida de Prada et al. (2017) “Demographics, epidemiology and the impact of vaccination campaigns in a measles-free world – Can elimination be maintained?”, Vaccine vol 35 issue 11 pg 1488-1493.

Los comentarios están cerrados.